지도학습에서 학습된 Model이 내놓는 예측값의 경향을 표현하는 척도로 Bias와 Variance를 사용한다.
Bias
Bias(편향)은 학습된 Model의 예측값과 실제값(정답)과의 차이를 나타내는 값이다.
model이 단순하면 training data를 제대로 학습하지 못하므로 Bias가 크다 (underfitting)
Variance
Variance(분산)은 학습된 Model의 예측값과 이 Model의 예측값 평균과의 차이를 나타내는 값이다. 즉, 예측값의 흩어진 정도를 나타낸다 (높을 수록 흩어진 모습을 보여준다)
model이 복잡하면 variance가 크고 training data의 특성은 잘 반영하지만, 학습하지 않은 data에 대해서는 오류가 크다. (overfitting)
다음과 같은 분류 model을 예시로 Bias와 Variance에 대해서 설명하자면, 아래 그림은 각각 3가지의 서로 다르게 학습된 model이 같은 data에 대해서 내놓은 분류이다.
각 값은 다음과 같은 것을 설명하고 있다.
X, O : 실제 값(정답)
파란선 : 모델이 내놓은 예측값(선을 기준으로 둘로 나눈다)

Bias와 Variance는 Model이 복잡하게 생긴 정도와 큰 관련이 있다.
1번 그래프와 같이 model이 너무 간단하게 학습되면 제대로 분류를 하지 못한다.
반대로, 3번 그래프와 같이 model이 해당 data에 맞게 너무 복잡하게 학습되면(과도하게 학습되면) 해당 data에 대해서는 잘 분류를 하지만, 나중에 다른 data가 들어오면 제대로 분류하지 못한다.
즉, model의 Variance가 너무 커서도 안되고 Bias가 너무 커서도 안된다
Trade-off 관계
그렇다면, Bias도 작게하고 Variance도 작은 model을 만들면 최고가 아닐까?
안타깝게도 Bias와 Variance는 trade-off 관계로 한 쪽이 낮아지면 다른 한 쪽이 올라가는 관계이다. 이 둘의 관계를 보기 위해 다음 식과 그래프를 보면 된다.
다음 식의 첫 항이 Bias이고, 두번째 항이 Variance를 나타낸다.
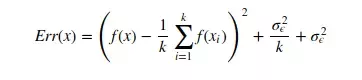
이를 나타낸 그래프는 다음과 같다.
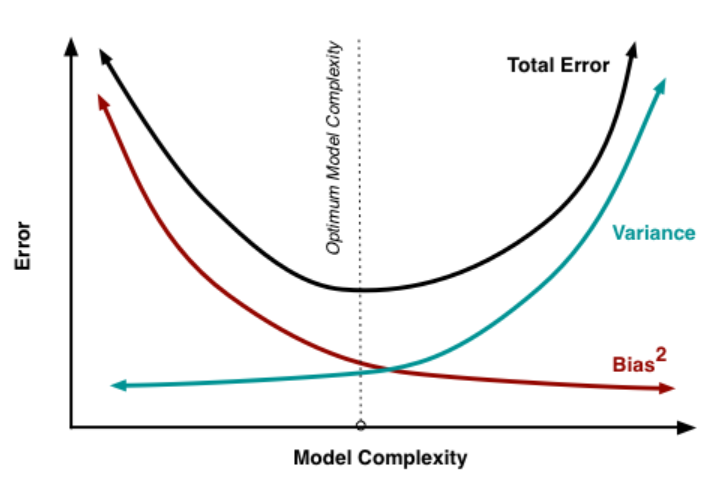
학습을 시킬수록 Bias는 줄어들고, Variance는 늘어난다.
학습을 덜 할수록 Bias는 늘어나고, Variance는 줄어든다.
Model의 Total Error를 낮추기 위해서, 적당히 학습하여 적당한 Bias와 Variance를 가지도록 한다.
'CS 지식 > 딥러닝 및 응용' 카테고리의 다른 글
| [필기] 학습에서 고려해야 할 것들 (0) | 2024.04.25 |
|---|---|
| [필기] Deep Neural Network (0) | 2024.04.25 |
| [필기] 신경망의 기초 with Shallow Neural Network (0) | 2024.04.25 |
| [필기] Learning의 기초 with Logistic Regression (0) | 2024.04.25 |
| Logistic Regression 코드 구현 (0) | 2024.04.06 |