Gauss-Seidel-type Iteration(GS)를 그대로 사용할 때 문제점
Gauss-Seidel-type Iteration(GS)을 그대로 사용할 때는 다음과 같은 문제점이 있다.
3N개의 unknown position component에 대해 M개의 방정식을 해결해야 하는데 (N개의 position, M개의 constraint)
- M ≥ 3N이면 over-determined, M ≤ 3N이면 under-determined.
- 방정식들이 일반적으로 비선형(GS는 선형 풀이법)
- 방정식이 아닌 부등식을 풀어야 할 때도 존재함.
다음의 예시를 통해 GS를 그대로 사용할 때의 문제점을 살펴보자.
p : position vector
Δp : correction vector, constraint을 만족하도록 position을 움직인 정도
다음과 같이 비선형 방정식, 부등식을 근사할 수 있음.
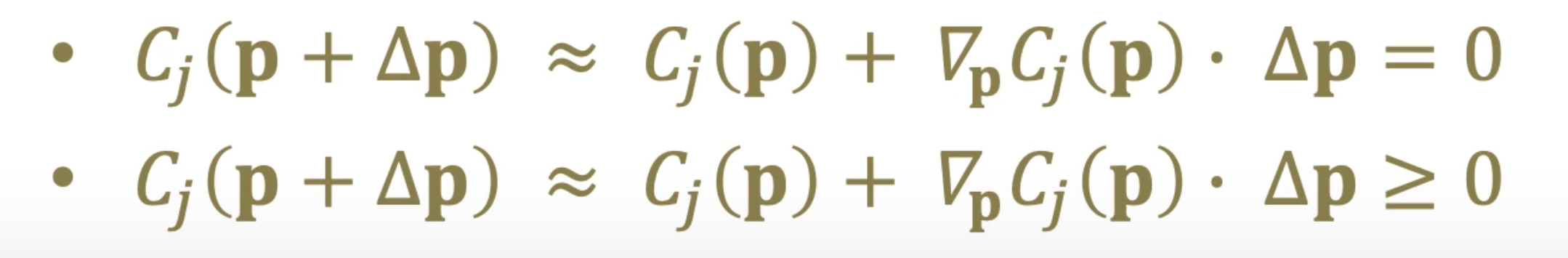
이 중에서 방정식은 global correction vetctor Δp에 대해서 다음과 같이 나타낼 수 있다.
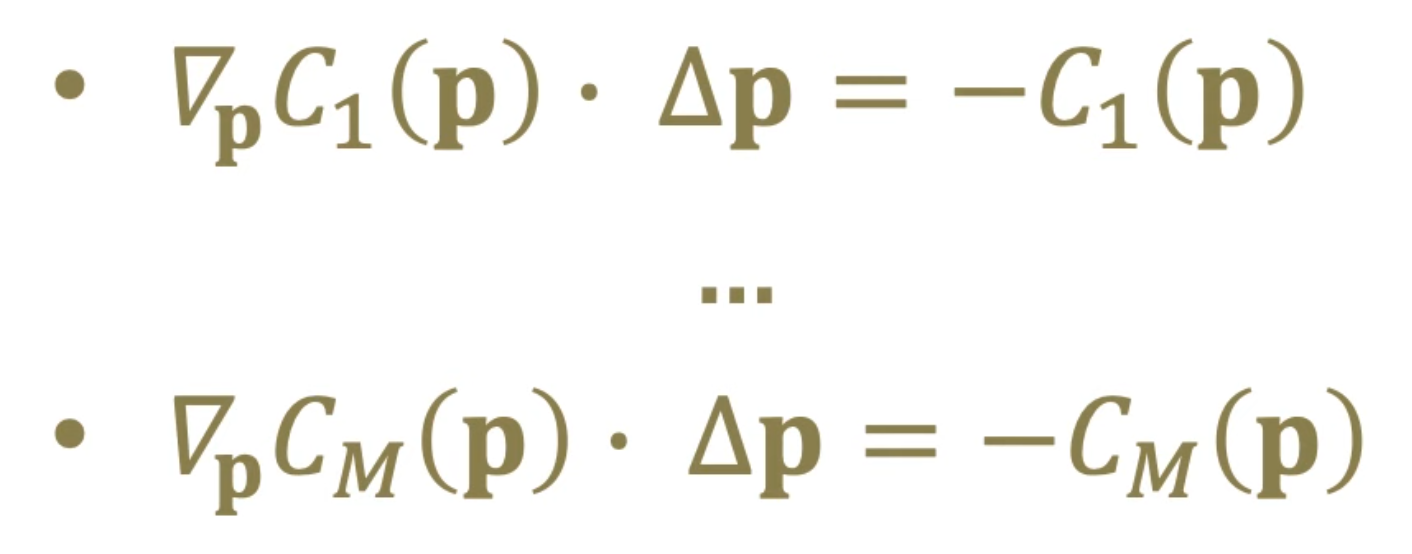
이렇게 근사된 식을 가지고, GS type iteration을 방정식마다 사용하여 Δp를 구할 수 있다.
그러나, unknown position component를 사용하므로 부정방정식(해를 하나로 정할 수 없는 방정식)이 됨. 선형 시스템을 통채로 Pseudo inverse를 이용하여 구할 수는 있지만, 이 방법을 사용해도 직접적으로 부등식을 해결할 수는 없다.
이러한 GS를 그대로 사용했을 때의 under-determined 문제와 부등식 문제를 해결하기 위해서 Δp를 constraint 방향으로 제한할 것이다.
Constraint에 따라 point들을 projection한다는 의미는 constraint를 만족하도록 점들을 이동하는 것을 의미한다.
이때, 점들을 이동시키는 것과 관련해서 가장 중요한 문제는 선운동량(linear momentum)과 각운동량(angular momentum)을 보존하는 것이다.
선운동량은 다음 식을 만족하면 보존된다. 이것은 질량 중심을 보존하는 것과 같다.
각운동량은 다음 식을 만족하면 보존된다. r_i는 임의의 공통 회전 중심까지의 p_i의 거리이다.
projection이 이러한 두 식을 모두 만족하지 않는다면, 물체를 끌거나 회전시키는 알 수 없는 외력(ghost force)이 추가된다.
이때, internal constraint만 운동량을 보존하면 되고, 충돌과 부착 constraint는 ojbect에 global 영향을 미치는 것이 허용된다. 이 논문이 제안하는 constraint projection 방법은 interanl constraint들에 대해 2가지 운동량을 모두 보존한다. 이러한 position based 방법은 constraint 함수를 직접 사용할 수 있기 때문에 force based 방법보다 더 직접적이다.
Δp를 constraint 방향으로 제한한다는 의미?
constraint 방향은 constraint gradient를 의미. constraint를 미분한다는 것은 constraint의 normal vector를 얻을 수이 있다는 의미. 즉, Δp를 constraint 방향으로 제한한다는 의미는 particle을 constraint를 만족하는 가장 빠른 방향으로 움직이게 한다는 것을 의미한다. 이것이 projection의 방향이 됨.
(constraint C(p) = |p| - d = 0 으로 고정된 함수에서 gradient vector의 의미는 해당 평면의 접점에 의해 형성되는 접 평면에 대한 법선 벡터를 나타냄.)
internal constraint은 rigid body mode(회전, 이동)과 무관하다. 이는 point를 회전하거나 이동하더라도 constraint 함수 값이 변경되지 않는다는 것을 의미한다. 즉, p에 대한 constraint의 기울기는 최대 변화 방향이기 때문에 rigid body mode에 수직이다. 이는 rigid body mode 방향으로 움직여도 constraint 값이 바뀌지 않으므로, constraint가 최대 변화 방향이면 rigid body mode와 아예 무관하게(수직으로) 움직인다는 뜻이다.
Constraint Projection
Δp를 constraint gradient 방향으로 제한한다는 것은, 제일 빠르게 constraint를 만족하는 방향으로 움직인다는 뜻이며, 이는 rigid body mode를 고려하지 않는다는 뜻이다. 단순히, particle들은 rigid body mode를 고려하지 않고, ∇C 방향으로 움직인다 라고만 생각하면 된다.
만약 Δp가 ∇C를 따라 선택된다면 모든 질량이 같을 때, 두 운동량(선운동량, 각운동량)은 자동으로 보존된다. 즉, p가 주어졌을 때, C(p + Δp) = 0이 되는 Δp를 구하고자 함.
particle들의 집합 p에 대해서 constraint C를 만족하는 Δp를 찾기 위해서 다음과 같은 과정을 거친다.
- C(p+Δp)를 근사한 다음과 같은 식을 구한다.
- 의미상으로 Δp는 constraint를 만족하는 방향으로 움직이므로 scalar λ에 대해서 다음과 같이 나타낼 수 있다.
- 식 1의 Δp를 식 2로 나타내고, 이를 λ에 대해서 나타낸 뒤, 이 λ에 대한 식을 식 2에 넣어 λ가 없는 Δp에 대한 식을 얻는다. (식 1에서 바로 Δp를 얻을 수 없는 이유는 ∇C를 분자로 넣을 수 없기 때문이다)
※ 람다는 라그랑그 승수.
'논문 리뷰 > Position Based Dynamics' 카테고리의 다른 글
| [Position Based Dynamics] 3.3. Constraint Projection (2) (0) | 2024.04.11 |
|---|---|
| [Position Based Dynamics] 3.3. Constraint Projection (3) (0) | 2024.04.09 |
| [Position Based Dynamics] 3.2. The Solver (0) | 2024.03.19 |
| [Position Based Dynamics] 3.1. Algorithm Overview (0) | 2024.03.10 |
| [Position Based Dynamics] 2. Related Work (0) | 2024.03.06 |





